[데이터구조 & 알고리즘] Quick Sort - 퀵 정렬 개요

배열을 정렬하는 데는 여러 가지 방법이 있다.

정렬이란 순서대로 나열하는 것을 의미한다.

 

[3, -2, -1, 0, 2, 4, 1]

위 배열을 정렬하면 

[-2, -1, 0, 1, 2, 3, 4]

가 된다.

 

그 중 Quick Sort(퀵 정렬)에 대해 알아보자.

퀵 정렬은 pivot을 정해 배열을 분할하여 정렬하는 방식이다.

 

 

코드는 아래와 같다.

 

def qs(arr, l, r):
	if l >= r: // 작거나 같으면 정렬할 필요 없음
    	 return
    p = partition(arr, l, r)
    
    qs(arr, l, p - 1)
    qs(arr, p + 1, r)

 

l, r은 정렬할 범위를 나타내는 인덱스이다.

l = r 이면 요소가 같아 정렬할 필요가 없고,

r < l 이면 정렬할 요소가 없다.

두 가지 경우에는 반환하여 끝난다.

 

그 다음 재귀함수(recurssive function)를 사용하여 정렬해준다.

3가지 인수(arr, l, r)를 받는 파티션 함수(분할)를 사용한다.

 

def qs(arr, l, r):
	if l >= r: // 작거나 같으면 정렬할 필요 없음
    	 return
    p = partition(arr, l, r)
    // 위의 파티션 함수 설명

파티션 함수는 첫 번째로 pivot을 정한다. pivot은 주로 마지막 인덱스인 r로 정해진다.

 

그러면 pivot보다 작은 숫자와 큰 숫자가 그룹으로 나누어지고

작은 숫자는 pivot의 왼쪽에 위치하게 되며

큰 숫자는 pivot의 오른쪽에 위치하게 된다.

[3, -2, -1, 0, 2, 4, 1]
// partition(arr,0,7) 함수 실행 후
[-2, -1, 0, 1, 2, 4, 3]

위를 보면 pivot이 1인 경우

왼쪽에는 1보다 작은 숫자, 오른쪽에는 1보다 큰 숫자가 오는 것을 볼 수 있다.

두 그룹 내 순서는 신경쓰지 않는다.

그 뒤 pivot(1)의 인덱스를 반환한다(위의 경우 3).

 

p = partition(arr, l, r)
// 반환된 인덱스 값을 p에 할당

이 함수의 실행이 끝나면 pivot의 위치가 확정된다.

파티션 함수를 실행한 뒤에는 양 옆 그룹 내 순서를 정렬해주기만 하면 된다.

 

위의 그림과 같이 pivot이 1일때 파티션을 나누면 (1)과 (2)의 그룹으로 나누어지고

재귀함수로 (1)그룹과 (2)그룹의 순서를 정렬해준다.

 

이제 다시 퀵정렬 코드를 살펴보자.

def qs(arr, l, r):
	if l >= r: // 작거나 같으면 정렬할 필요 없음
    	 return
    p = partition(arr, l, r)
    //l,r 범위에서 pivot을 기준으로 큰 수와 작은 수를 나누어 pivot의 인덱스 값을 p에 할당
    
    
    qs(arr, l, p - 1) //사진의 1부분 정렬(재귀함수), 위에서 반환된 피벗 왼쪽 정렬
    qs(arr, p + 1, r) //사진의 2부분 정렬(재귀함수), 위에서 반환된 피벗 오른쪽 정렬

위와 같은 방식으로 재귀함수가 호출되어 전체 배열이 정렬된다.

pivot을 정하여 양쪽 그룹을 나누고, 또 각 양쪽 그룹마다 pivot을 정하여 그룹을 나누어 가다보면

전체 배열이 정렬된다는 원리이다.

 

그럼 partition 함수는 어떻게 작동하는지 알아보자. 

그림과 같이

10이 피벗일 때 i,j 인덱스를 사용한다.

l 부터 r-1(피벗 직전)까지 배열의 요소를 검사한다.

i까지는 피벗보다 작은 그룹, j까지는 피벗과 같거나 큰 그룹

즉, i는 피벗보다 작은 숫자를 가르켜야 하고 j는 피벗보다 큰 숫자를 가르켜야 한다.

 

만약 j가 피벗보다 작은 숫자를 가르키면 j가 가르키는 요소와 i의 다음 [i+1] 인덱스의 요소와 바꾼다.

그렇게 i과 j를 비교해 나가면 두 그룹으로 나뉜다. 

마지막으로 피벗을 i+1 배열의 인덱스(피벗보다 작은 요소 다음 인덱스)와 바꿔주면 피벗은 중간으로 들어가게 된다.

 

배열, l, r의 3개의 인수를 받는 partition 함수의 코드를 살펴보자.

def partition(arr, l, r):
	pivot arr[r]
    i = l - 1;
    for j from l upto r - 1;
    	if arr[j] < pivot:
        	i += 1
            swap arr[i] and arr[j]
    swap arr[i+1] and arr[r]
    return i + 1 //index of the pivot

 

 

퀵정렬 재귀함수가 이해되지 않는다면 다음 이미지를 참조하자.

아래 이미지는 내가 작성한 방식과는 약간 다른다.

피벗을 기준으로 양쪽에서 줄어들며 서로 비교하는 방식인데 딱히 다른 건 없다.

중요한건 피벗을 기준으로 작은 수와 큰 수를 나누어 두가지 그룹으로 분리한다는 것이 핵심이다.

Quick Sort(퀵정렬) Java(자바) 코드

package src;

public class TestQuicksort {
    public static void main(String[] args) {
        int[] a1 = {1, 2, 3};
        int[] a2 = {3, 2, 1};
        int[] a3 = {};
        int[] a4 = {3, 1, -1, 0, 2, 5};
        int[] a5 = {2, 2, 1, 1, 0, 0, 4, 4, 2, 2, 2};
        int[] a6 = {0};
        int[] a7 = {3, -2, -1, 0, 2, 4, 1};
        int[] a8 = {1, 2, 3, 4, 5, 6, 7};
        int[] a9 = {2, 2, 2, 2, 2, 2, 2};

        int[] a1Sorted = {1, 2, 3};
        int[] a2Sorted = {1, 2, 3};
        int[] a3Sorted = {};
        int[] a4Sorted = {-1, 0, 1, 2, 3, 5};
        int[] a5Sorted = {0, 0, 1, 1, 2, 2, 2, 2, 2, 4, 4};
        int[] a6Sorted = {0};
        int[] a7Sorted = {-2, -1, 0, 1, 2, 3, 4};
        int[] a8Sorted = {1, 2, 3, 4, 5, 6, 7};
        int[] a9Sorted = {2, 2, 2, 2, 2, 2, 2};

        quicksort(a1);
        quicksort(a2);
        quicksort(a3);
        quicksort(a4);
        quicksort(a5);
        quicksort(a6);
        quicksort(a7);
        quicksort(a8);
        quicksort(a9);

        assert arrayEquals(a1, a1Sorted);
        assert arrayEquals(a2, a2Sorted);
        assert arrayEquals(a3, a3Sorted);
        assert arrayEquals(a4, a4Sorted);
        assert arrayEquals(a5, a5Sorted);
        assert arrayEquals(a6, a6Sorted);
        assert arrayEquals(a7, a7Sorted);
        assert arrayEquals(a8, a8Sorted);
        assert arrayEquals(a9, a9Sorted);
        System.out.println("If you didn't get an assertion error, this program has run successfully.");
    }

    static void quicksort(int[] arr) {
        qs(arr, 0, arr.length - 1);
    }

    static void qs(int[] arr, int l, int r) {
        if (l >= r) {
            return;
        }
        int p = partition(arr, l, r);

        qs(arr, l, p - 1);
        qs(arr, p + 1, r);
    }

    static int partition(int[] arr, int l, int r) {
        int pivot = arr[r];
        int i = l - 1;
        for (int j = l; j < r; j++) {
            if (arr[j] < pivot) {
                i += 1;
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        int temp = arr[i + 1];
        arr[i + 1] = arr[r];
        arr[r] = temp;
        return i + 1;
    }

    // 두 배열이 동일한 지 다른 지 검사
    static boolean arrayEquals(int[] a1, int[] a2) {
        if (a1.length != a2.length) {
            return false;
        }
        for(int i = 0; i < a1.length; i++) {
            if (a1[i] != a2[i]) {
                return false;
            }
        }
        return true;
    }
}

 

Time Complexity(시간 복잡도)

 

1. Worst Case

 

[1, 2, 3, 4, 5, 6, 7] - 매차례 돌아가면서 비교해야할 때

[2, 2, 2, 2, 2, 2, 2]

 

 qs(arr, 0, 6) -> qs(arr, 0, 5) -> qs(arr, 0, 4) -> ... -> qs(arr, 0, 1)

 

2. Best Case & Average Case

 

[-2, 3, -1, 5, 4, -3, 0] - pivot 보다 작은 수와 큰 수가 동일하게 있을 때

 

 

 

---

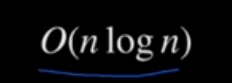
1. Pivot을 선택하는 방법

- 마지막 요소 선택

- 랜덤 요소 선택(위의 퀵소트 정렬을 하기 전에 배열을 셔플하여 실행)

- 3개의 요소를 랜덤으로 선택한 후 중간 요소를 선택

 

2. 중복을 해결하는 방법

- 3-Way Quicksort. (Less/Equal/High)

www.geeksforgeeks.org/3-way-quicksort-dutch-national-flag/

3-Way QuickSort (Dutch National Flag) - GeeksforGeeks

 

퀵 정렬의 루프는 컴퓨터 아키텍처에서 효율적으로 작동하도록 설계되어 있다.
메모리 참조가 지역화되어 있어 CPU 캐시의 히트율이 높아지기 때문에 worst case의 시간 복잡도에도 불구하고 많이 사용한다.